Types of Data Science Questions

In approximate order of difficulty

• Descriptive
• Exploratory
• Inferential
• Predictive
• Causal
• Mechanistic

Goal: Describe a set of data

• The first kind of data analysis performed
• Commonly applied to census data
• The description and interpretation are different steps
• Descriptions can usually not be generalized without additional statistical modeling

http://www.census.gov/2010census/

http://books.google.com/ngrams

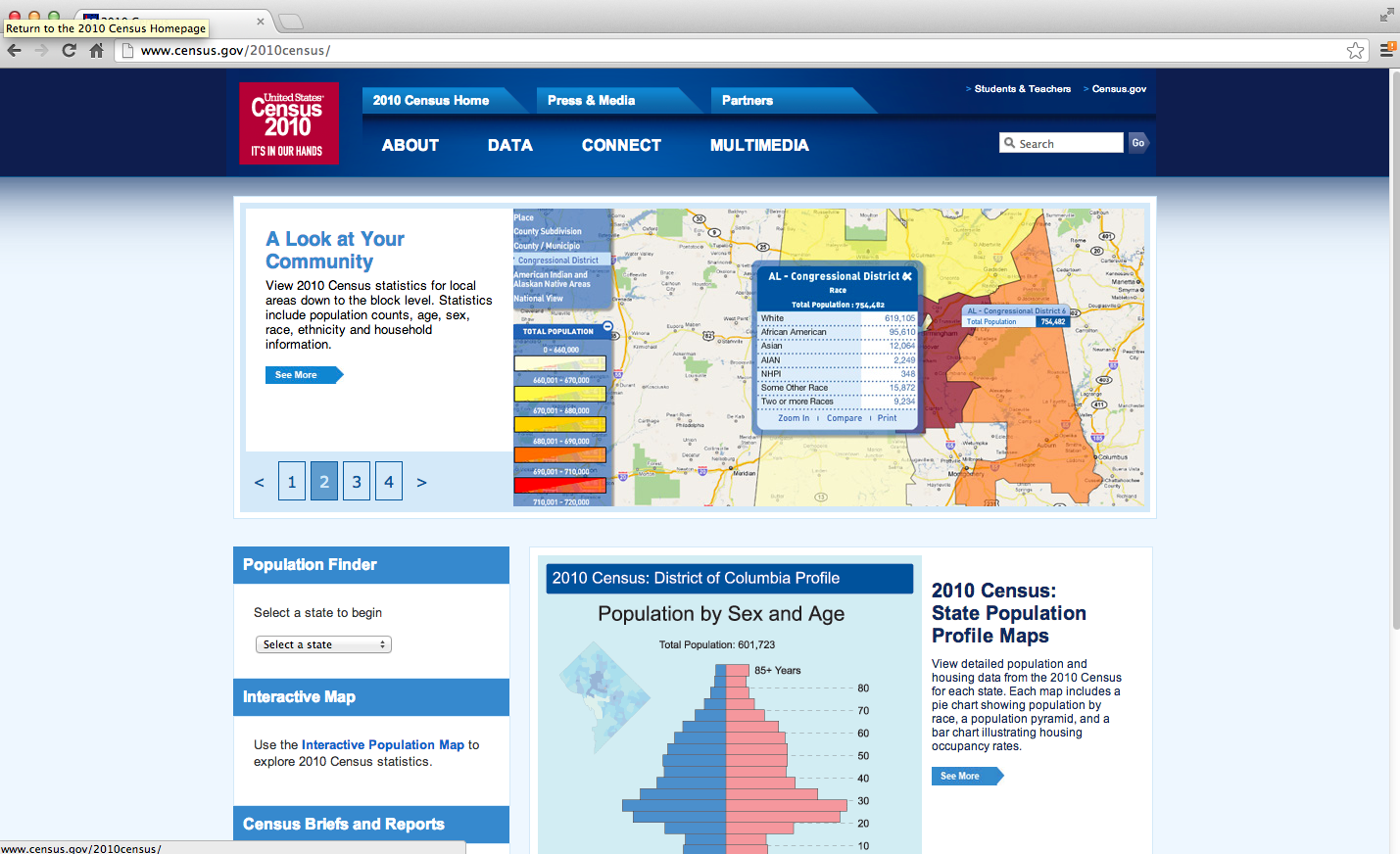
Goal: Find relationships you didn't know about

• Exploratory models are good for discovering new connections
• They are also useful for defining future studies
• Exploratory analyses are usually not the final say
• Exploratory analyses alone should not be used for generalizing/predicting
• Correlation does not imply causation

Liu et al. (2012) Scientific Reports

http://www.sdss.org/

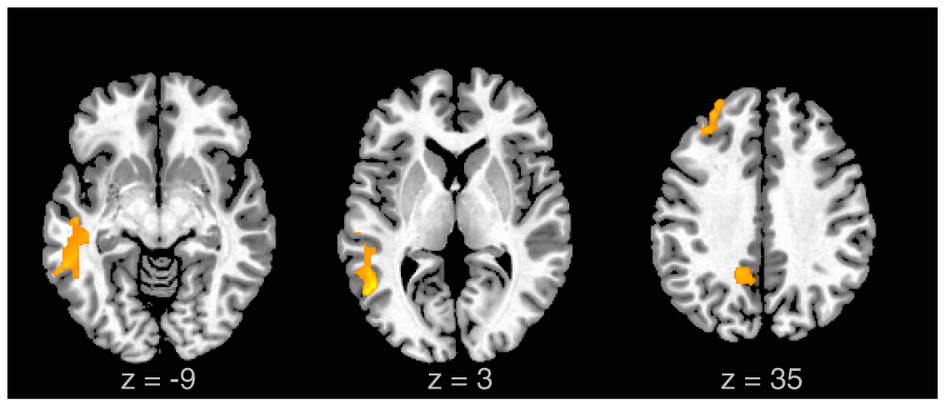
Goal: Use a relatively small sample of data to say something about a bigger population

• Inference is commonly the goal of statistical models
• Inference involves estimating both the quantity you care about and your uncertainty about your estimate
• Inference depends heavily on both the population and the sampling scheme

Correia et al. (2013) Epidemiology

Goal: To use the data on some objects to predict values for another object

• If \(X\) predicts \(Y\) it does not mean that \(X\) causes \(Y\)
• Accurate prediction depends heavily on measuring the right variables
• Although there are better and worse prediction models, more data and a simple model works really well
• Prediction is very hard, especially about the future references

http://fivethirtyeight.blogs.nytimes.com/

http://www.forbes.com/sites/kashmirhill/2012/02/16/how-target-figured-out-a-teen-girl-was-pregnant-before-her-father-did/

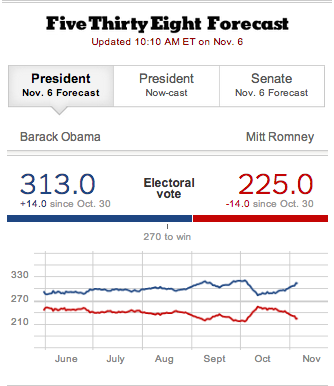
Goal: To find out what happens to one variable when you make another variable change.

• Usually randomized studies are required to identify causation
• There are approaches to inferring causation in non-randomized studies, but they are complicated and sensitive to assumptions
• Causal relationships are usually identified as average effects, but may not apply to every individual
• Causal models are usually the "gold standard" for data analysis

van Nood et al. (2013) NEJM

Goal: Understand the exact changes in variables that lead to changes in other variables for individual objects.

• Incredibly hard to infer, except in simple situations
• Usually modeled by a deterministic set of equations (physical/engineering science)
• Generally the random component of the data is measurement error
• If the equations are known but the parameters are not, they may be inferred with data analysis

http://www.fhwa.dot.gov/resourcecenter/teams/pavement/pave_3pdg.pdf